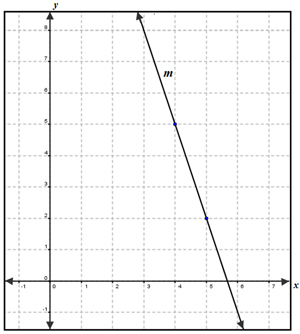
Line m is shown on the coordinate grid below.

Which equation best represents the line that is parallel to the graph of the line m?

A. -3x + 7 = 17
Incorrect. The y-intercepts are the same in these equations, but the slopes must be the same to be parallel.

B. y = 1 3 x + 4
Incorrect. These two lines are perpendicular because their slopes are negative reciprocals.

C. y = -3x + 4
Correct! The slopes must be the same for the lines to be parallel!

D. y = - 1 3 x + 4
Incorrect. The slopes on these two lines are just reciprocals. They need to be the same to be parallel.

Which of the following best describes the graph of the equations below?

x − 2y = -6

2x + y = 2

A. The lines have the same x-intercept.
Incorrect. Remember the x-intercept is where the line crosses the x-axis.

B. The lines are perpendicular.
Correct! The slopes were negative reciprocals of each other.

C. The lines are parallel.
Incorrect. Remember the lines are parallel only when the slopes are the same.

D. The lines have the same y-intercept.
Incorrect. Remember the y-intercept is where the line crosses the y-axis.

Which graph below represents the line passing through (4, 1) and perpendicular to -2x + y = -3?
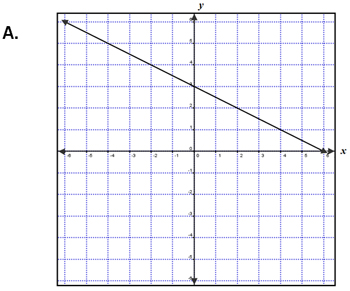Correct! The slopes of perpendicular lines are negative reciprocals.	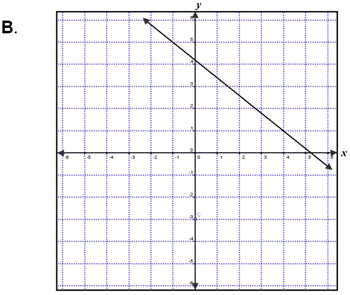Incorrect. While this line does pass through the correct point, the slope isn’t right, remember it needs to be the negative reciprocal of the original slope.
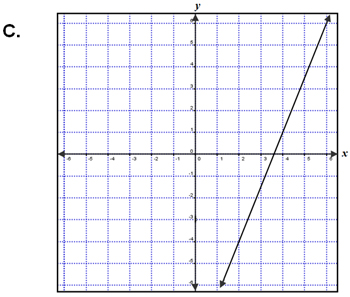Incorrect. While this line does pass through the correct point, the slope isn’t right, remember it needs to be the negative reciprocal of the original slope.	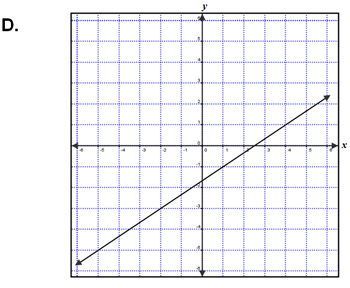Incorrect. While this line does pass through the correct point, the slope isn’t right, remember it needs to be the negative reciprocal of the original slope.

Which graph below represents a line that is parallel to the graph of the equation 5x + 2y = 1?
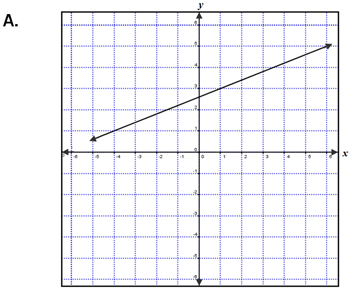Incorrect. You found the slope of the perpendicular line, remember the slopes are the same in parallel lines.	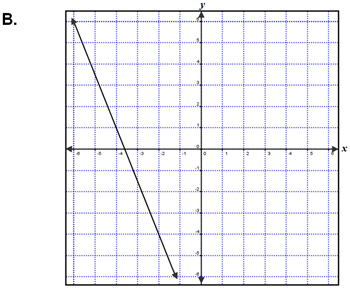Correct! The slopes of parallel line must be the same.
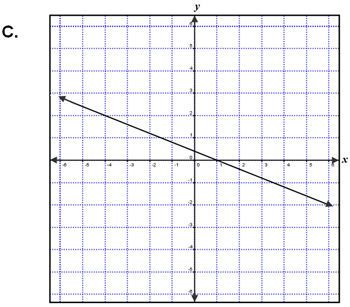Incorrect. You have the correct sign, the slope should be negative, but you need the reciprocal to have the right answer.	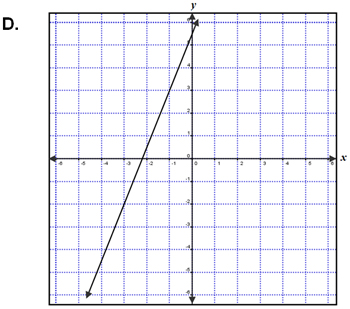Incorrect. You have the correct absolute value of the slope but forgot the sign must be negative.